Recientemente compartía una serie de recursos para motivar el tema de la probabilidad en el aula, un área que tiene cierto éxito entre otros temas del libro. Comentaba que cuando se empiezan a introducir conceptos de teoría de conjuntos, combinatoria y otras formulas, muchas veces el interés por el tema ya no es el mismo. En la actividad TIC para el aula de matemáticas que propongo esta semana, se dan por estudiados ya varios conceptos de probabilidad (sucesos, Regla de Laplace, frecuencias, etc.) Es una actividad con la que el alumno puede comprobar por sí mismo, a través de simulaciones, como se cumple, por ejemplo, la Ley de los Grandes Números.
¿Cuál es la probabilidad de sacar un «6» con un dado? Suponemos, lógicamente, un dado de 6 caras, con las caras numeradas del 1 al 6 y en el que todas los posibles resultados (sucesos elementales) son igualmente probables (equiprobables). Todos diríamos 1 de 6, es decir, un 16,67 % de probabilidad de sacar un «6», o cualquiera de los posibles resultados. Acabamos de aplicar la Regla de Laplace para el cálculo de probabilidades: simplemente dividiendo el número de casos favorables (1, porque solo hay un «6») entre el número de casos posibles (6, porque hay 6 posibles valores), obtenemos dicha probabilidad.
Pero, ¿qué sucedería si repitiéramos el experimento de lanzar un dado varias veces, por ejemplo, 10? En cada lanzamiento, la probabilidad seguiría siendo del 16,67%, y podría salir el «6» o no. Podrían salir diez «6» o ninguno en los 10 lanzamientos. 10 es un número pequeño.
 Sin embargo, ¿qué sucedería si en lugar de 10 lanzamientos repetimos el experimento con 100? ¿y con 1000? Bien, aquí entra en juego la Ley de los Grandes Números, que dice así:
Sin embargo, ¿qué sucedería si en lugar de 10 lanzamientos repetimos el experimento con 100? ¿y con 1000? Bien, aquí entra en juego la Ley de los Grandes Números, que dice así:
«La frecuencia relativa de un suceso tiende a estabilizarse hacia una constante a medida que se repite el experimento.»
Recordemos que la frecuencia relativa de un suceso A (obtener un «6»), al realizarse un experimento N veces, se obtiene de dividir la frecuencia absoluta (las veces que sale el «6»), dividido por el número total de veces que se ha repetido el experimento.
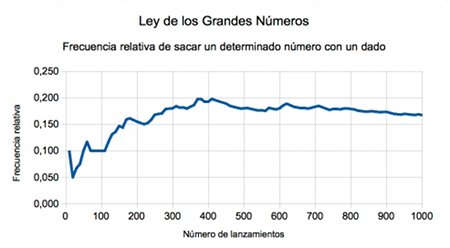
Y, ¿hacia qué valor constante tiende a estabilizarse la frecuencia relativa del suceso «obtener un 6» cuando repetimos el experimento, por ejemplo, 1000 veces. Puedes comprobarlo en la gráfica, resultado de una simulación realizada con un hoja de cálculo, y que es el objetivo de esta actividad.
El valor se aproxima a algo más de 0,15, exactamente 0,167. ¿No es curioso que coincida con el valor que habíamos calculado con la Regla de Lapace? Y es que:
«La probabilidad de un suceso es la constante a la que se aproxima la frecuencia relativa cuando el experimento se repite muchísimas veces.»
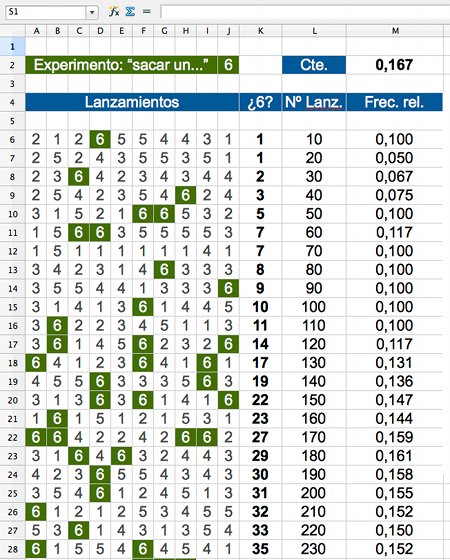
Con el objetivo de comprobar que efectivamente la Ley de los Grandes Números se cumple, propongo una actividad para trabajar con las TIC, que consiste en diseñar una hoja de cálculo capaz de simular el experimento de lanzar “N” veces un dado.
La hoja de cálculo agrupará los lanzamientos de 10 en 10, para ir calculando automáticamente las veces que se obtiene un determinado resultado y la frecuencia relativa de tal suceso. Finalmente, se generará con el programa una gráfica que mostrará cómo la frecuencia relativa tiende a una constante.
La actividad
En el siguiente documento (PDF, 4 páginas), está detallada la actividad y las fórmulas de hoja de cálculo necesarias para generar números aleatorios y realizar los cálculos de frecuencias.
Actividad | La Ley de los Grandes Números (PDF, 4 páginas)
En Tiching | La Ley de los Grandes Números
Software | LibreOffice.org (incluye Calc, para diseño de hojas de cálculo)
Imagen Dados | Dice de Swiss Bones en Flickr


4 Comments
[…] el experimento de lanzar un dado. Existen 6 posibles resultados: 1,2,3,4,5 y 6. En un primer ejemplo, supongamos también dos […]
[…] El resultado obtenido se acercará tanto más al esperado cuanto mayor sea el número de veces que hagas la prueba. (Ley de los grandes números). […]
Me parece una actividad excelente, ideal para fomentar el gusto por las matemáticas, disminuir la apatía de los estudiantes por la probabilidad y añadir el uso de las TICs. Me encantó la aportación. Muchas gracias.
Buenos dias:
Excelente ejercicio para entender y aplicar el concepto de la Ley de los grandes números.
Saludos